
Problems for
Intermediate Methods in Theoretical Physics
Edward F. Redish
 |
Problems for Edward F. Redish |
| A small toy train is running around a circular track. The train is powered by a wind-up spring in the engine. In an alternate universe version of this exam you estimated the amount of energy stored in the train's spring. If you want to have an idea how long the train will run, you need to calculate what dissipative mechanisms there are. |
 |
In this universe, you need to estimate the amount of work done by friction on the train as it goes around one loop of the track. Assume the train travels at a constant speed, v , has a mass m , the track has a radius R , and the coefficient of friction between the train and the track governing loss of the train's kinetic energy is μ. (The issue of friction is actually quite tricky here, since the rolling of the train requires friction. Perfect friction would mean no slippage and no loss. Ignore this and assume we have taken this all into account in constructing a value for μ.)
(a) Calculate the amount of work done by friction on the train as it travels once around the track.
(b) Calculate the rate at which the spring must provide energy in order to overcome the energy lost to friction calculated in part (a).
(c) Do you think this is a good model for the energy loss of the train or do you think there are other loss mechanisms that should be included? If you think it is a good model, explain why. If you think there are other mechanisms, mention one.
Solution
(a) The work done in moving a small distance is F⋅ds. Since the frictional force is opposite to the direction of the velocity, the result is just -F ds. The force is μ N where N is the normal force squeezing the two surfaces together. In this case, N is the weight of the train, mg. The result is that for traveling a small distance along the track, ds, the work done by friction is just -μmg ds. Integrating around the distance of one loop, the result is:
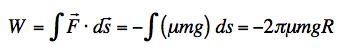 .
.
(b) The rate at which energy must be applied to the train to keep the kinetic energy from decreasing due to friction is
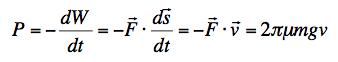
(c) It's not too bad a model but there are other mechanisms of loss. Two are the air drag that the train encounters and the loss of spring potential energy to internal friction as it unwinds.
| University of Maryland | Physics Department | Physics 374 Home |
|---|---|---|
 |
 |
 |
Last revision 16. October, 2005.