Problems for Intermediate Methods in Theoretical Physics Edward F. Redish

In a plasma, for a short time, the electric field is well described by the function where C is a constant.   This field arises from both charges and from changing magnetic fields, so we cannot assume that there is a well-defined potential function for E.   (a) Evaluate   around the loop shown at the right for the given electric field by doing the line integrals explicitly.

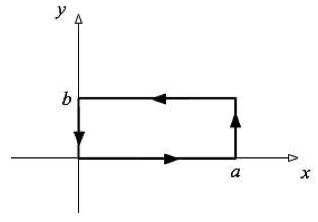(b) If we were to carry a charge, q , around the loop shown in the direction shown, what would be the work done by the electric field on the charge?

Solution

(a) Let's break the integral up into four parts, one along each leg:

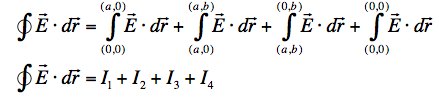
Since along the first leg, x remains 0 everywhere along the leg, the E-field vanishes at every point on the first leg so I₁ = 0. Along the 4th leg, y remains 0 everywhere along the leg, so again, the E-field vanishes at every point on the fourth leg so I₂ = 0 as well.

Along the second leg, x = a at every point on that leg so we can substitute a for x for that integral. Along this leg, therefore,

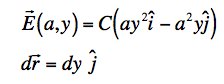
so the integral takes the value

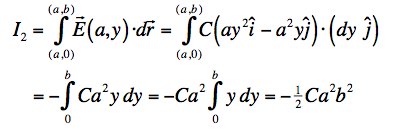
Along the third leg, y = b, so along this leg

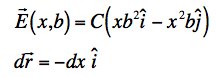
Notice that along this leg, I have put the direction of travel into the dr vector with a minus sign. That vector equation tells the way I am moving. As a result, I have to add up the integrands in a positive direction, doing the integral from 0 to a rather than the other way around. If I put the negative directional information in twice it will cancel and give me the wrong answer. We can do it either way, but I think it is easier to think of the integral as a sum of small bits. If the field and the displacement are at an angle of greater than 90o, the dot products will all be negative. Our integral is therefore the sum of lots of little negative numbers and the overall result should be negative.

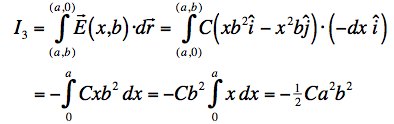
The total result is therefore the sum:

.

(b) The work is just the integral of the force rather than the field. Since F = qE, the result is straightforward:

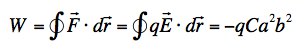
(This agrees nicely with the easier calculation using Stoke's theorem.)

RETURNS

University of Maryland	Physics Department	Physics 374 Home

Last revision 17. October, 2005.