Problems for
Intermediate Methods in Theoretical Physics

Edward F. Redish

Finding the Time Dependence of a String

The displacement of a bit of a transversely oscillating string satisfies the wave equation

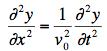  where  

T is the tension of the string and ρ is the mass density (mass per unit length) of the string.

(a) For a string connected between two fixed points at x = 0 and x = L , find the frequencies and shapes of the normal modes of the system. (Be sure to show how you get these conclusions starting from the information given.)

(b) Suppose at t ≤ 0, the string is held so that y(x,0) = f(x). At the time t = 0 the string is released.   Explain how you would go about finding y ( x,t ) for t > 0 and write equations that would allow you to calculate that function if you had a computer available.

RETURNS

University of MarylandPhysics DepartmentPhysics 374 Home

This page prepared by

Edward F. Redish
Department of Physics
University of Maryland
College Park, MD 20742
Phone: (301) 405-6120
Email: redish@umd.edu

Last revision 2. December, 2005.