
Problems for
Intermediate Methods in Theoretical Physics
Edward F. Redish
 |
Problems for Edward F. Redish |
The diffusion equation for the motion of a small particle in a fluid is
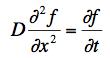
where D is a diffusion constant and f(x,t) is the number density of small particles per unit volume at the position x at a time t.
(a) From our experience with differential equations, we expect that f might be an exponential. But an exponential has to be a function of a dimensionless variable. Create a dimensionless variable, z, by combining the dimensioned space and time variables with the diffusion constant.(b) Let us model our small particles as tiny spheres of radius a. We expect that their jiggling around and subsequent diffusion is a result of the molecules of the fluid bumping into them in random ways. We also expect that their ability to get through the fluid depends on the resistance of the fluid. Let us model the fluid resistance by a viscous force, Fvisc = -bv, and note that the temperature is related to an energy by Boltzmann's constant,Θ = kBT. Express the diffusion constant D in terms of the lower-level system parameters a, b, and Θ.
(c) The diffusion constant, D , is a measure of how fast the small particles spread out; bigger D means more diffusion, smaller D less. From your results above, does the system behave as you expect as the temperature, T , increases? As the viscosity coefficient, b , increases? Explain.
| University of Maryland | Physics Department | Physics 374 Home |
|---|---|---|
 |
 |
 |
Last revision 8. November, 2005.