Problems for Intermediate Methods in Theoretical Physics Edward F. Redish

An elastic string is stretched and connected to two posts as shown in the picture below.   On one end it is fixed, on the other connected to a nearly frictionless ring.   Describe the system by the coordinate system shown.   The length of the string is L, it has a mass m, and is pulled taut to a tension T .   Assume the widths of the rod and ring, the mass of the ring, the friction between the rod and the ring, and gravity can all be ignored for this calculation.   Take the 0 of the x-y coordinate system to be at the point where the ring is tied to the left post.

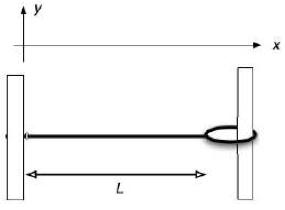(a) Write the equation of motion for the displacement of the bit of the string at the point x, y(x,t).

(b) What are the boundary conditions satisfied by the solution of this equation for the case described?

(c) Find the normal modes for the motion of this string.

(d) If the string starts at time t = 0 displaced into a shape f (x) that satisfies the boundary conditions, how would you find the shape of the string at a later time, t ?   Give enough detail that you could actually do the calculation if the function f were given.

RETURNS

University of Maryland	Physics Department	Physics 374 Home

Last revision 13. November, 2005.