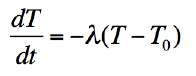 .
.You can, of course, solve this equation for the function T(t) analytically. But let's demonstrate how the Euler method works on this simple equation.
If we use the Taylor series to expand T(t + Δt) about t, we get:
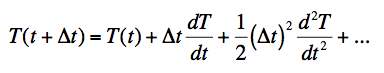 .
.Keeping only the first order term and putting the result into the original equation gives
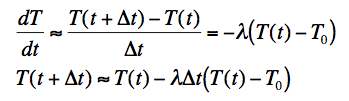 .
.In the last line above, we have solved for T(t + Δt) in terms of the value of T at an earlier time and the parameters of the system. This means we can "step." That is, if we know the values of the parameters (λ and T0) and the value of T at the starting time, we can use the above equation to find T at a time Δt later; we can then use that value to find T at a time Δt later, etc., etc., on into the future.
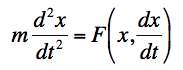 .
.This says that "ma" is equal to the net force which, typically, can be a function of the position and velocity. (Though we have expressed this in one-dimension for one mass for simplicity, the process is easily generalized to many dimensions and many particles.) To apply the Euler method, we have to have first order equations, so we introduce the velocity, v, as a second variable. This separates Newton's second order second law into two first order equations.
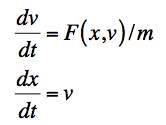 .
.We now have two first order equations in two unknowns (x and v) and we can apply the Euler approach to generate a stepping rule.
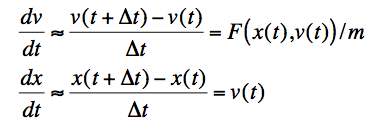
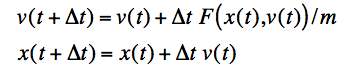 .
.
If we know the position and velocity at a time t, we can use them to calculate the force at that time and use that to calculate the position and velocity at a later time, t + Δt, stepping our knowledge to predict the future motion of the object.
| University of Maryland | Physics Department | Physics 374 Home |
|---|---|---|
 |
 |
 |
Last revision 24. September, 2005.