Dimensions

Dimensionless Equations

1. It is easier to recognize when to apply familiar mathermatical techniques.
2. It reduces the number of times we might have to solve the equation numerically.
3. It gives us insight into what might be small parameters that could be ignored or treated approximately.

1. In our discussion of Natural Scales, we point out that the creation of natural scales from the dimensioned parameters of our problem can often tell us what the form of an analytic solution will look like. Even if we can't solve something analytically and have to resort to a numerical solution, dimensional analysis and natural scales can help us by simplifying the equation dramatically. This simplification makes the equation look like "math" as taught in math classes without cluttering up things with lots of symbols -- symbols that are essential to understanding the relation of the equation to the physical system but that get in the way when trying to recognize the applicability of techniques learned in a math class or math book.

2. Another valuable result of using natural scales to simplify an equation occurs when we have to solve an equation numerically for many cases with different parameters. If we remove the parameters from the equation we are solving by using natural scales, we may find that solving the equation numerically once suffices for all the different cases we might have to solve. We will see this in the example below.

3. Sometimes our dimensional reduction will yield terms in our equation that can be immediately seen to be small under certain conditions. We can then know when to ignore them. For example, in our analysis of 1D motion of an object falling in air under the Newton Drag Law, we transform the original equation (v assumed > 0) into dimensionless form:

.

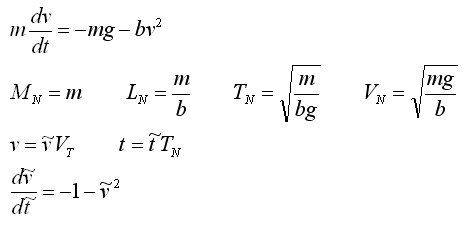We have taken our original parameters, m, g, and b, and constructed natural scales, M_N, L_N, and T_N. From these, we have constructed V_N = L_N/T._N. We have then introduced dimensionless variables (v-tilde and t-tilde), and rewritten the equation in terms of them. All of the dimensioned parameters drop out of the dimensionless equation.

We know, however, that the v-tilde squared term is the one corresponding to the air drag. We can easily see in this form, that the air drag can be neglected as long as

.

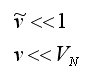Putting in the expression for V_N, we see that it satisfies

This reveals V_N as the terminal velocity and tells us that when throwing an object upward, we can ignore air drag if the initial velocity is much less than the object's terminal velocity in the air. This is not entirely obvious since terminal velocity was defined when the object was falling, but it seems a reasonable and natural conclusion.

In other cases, we may have more than one natural parameter of a given dimension. Their ratio then provides a dimensionless parameter which may tell which effects dominate a system. This can be a big help when trying to simplify a complex set of equations in fluid dynamics, plasma physics, or particle physics.

RETURNS

University of Maryland	Physics Department	Physics 374 Home