Considering Change
What our dimensional analysis is really about is change: How does the quantity we are talking about change when we change one of the arbitrary choices that we make in order to describe the universe? Considering change clarifies the reasons behind our principles of dimensional analysis.
Changing our scales
Dimensions are about the fact that we can make an arbitrary choice of unit when we define a kind of measurement operationally. Since this choice is arbitrary, we don't want the equations we write to represent some equality between physical objects to depend on how we choose to describe the world. ("A difference that makes not difference should make no difference!") This is true for purposes of communication, but it also gives us insight into the structure of reality.
Communication
One thing our whole mathematical structure is about is communication. We want to be able to express physical principles, relationships, and results in ways that are less ambiguous than our everyday speech and mathematical equations (and standard graphs and schematic pictures) help us do this. If you look at a physics text in a foreign language where you know the physics but do not know the language (even perhaps the characters or alphabet) you may well find that you can make out most of what is going on anyway.
But sometimes we take too much for granted in the universality of our use of mathematics. Many science papers become unreadable to a large fraction of their intended audience because the author incorrectly assumes "everyone uses the same symbols that I do" and fails to define terms clearly.
A particularly dangerous example of this is units. Occasionaly, scientists or engineers will fail to specify the unit system they are working with because they incorrectly assume "we're all using the same system." Tragically, NASA lost a $125 Million mars probe because two groups of engineers were using different units and each assumed that everyone was doing what they were so they didn't need to specify.
The Structure of the Way We See Reality: Functional dependence
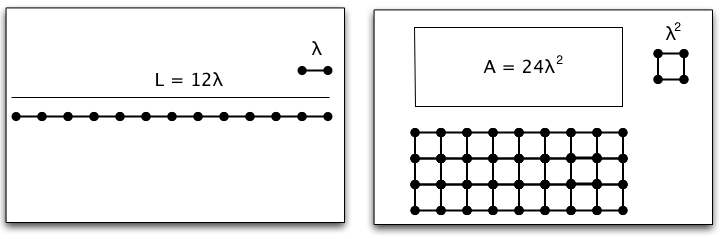
As an example, consider how we measure different kinds of physical space by comparing measurements of length and area. In both cases, we make a choice of a standard unit and count the number of times our unit fits in to get an assigned number. In the case of length, we use a small line segment, while in the case of area, we use a small box. Typically, we make the choice to make our area boxes squares with the side equal to our length segment. (This isn't absolutely necessary. Think about what we would have to do if we didn't do this.)
When we fit a length, the number of times our unit length, λ, fits in depends linearly on the length we choose. When we fit square boxes of unit area, λ2, the number of boxes we fit in depends quadratically on the length we choose.
To see what this means, imagine that instead of a length λ, we choose a different length, μ = λ/2. Our new measurements can be found algebraically in a straightforward way.
L = 12 λ = 12 (2 x λ/2) = 24 μ
A = 24 λ2 = 24 (2 x λ/2)2 = 24 x 4 (λ/2)2 = 96 μ2.
Note that we have to change λ inside the square when we are working with the area. This shows that if we change our unit scale for length, the length and the area change in different ways.
This clarifies the reason why we cannot equate a length and an area. Even if the number assigned to them agrees in one system, it will not in any other.
Active vs. Passive Transformations: Scaling
A viewpoint that makes these changes even more interesting is a switch from passive to active view. When we described why we wanted to make units match, we took a passive point of view. That is, we assumed that we had a fixed physical system and we were describing it in different units We could flip this and take an active point of view. That is, we could assume that we have a fixed unit and we were changing our system. Thus, instead of saying that we switched to a unit half as big, we could say we switched to a length or area twice as big in all dimensions. Our argument then shows that size of our length, doubles its measure of length (doh!), but that doubling the size of our area (in all dimensions), quadruples its measure of area. This has powerful practical implications. (For an example, see the scaling problem.)
How things change when we change some of the input descriptors is a general and powerful method in advanced research physics. The general technique is associated with group theory: the mathematical tools for studying how things change. For example, general relativity was developed from Einstein's idea that the equations of physics should remain the same under any change of coordinates -- even complicated non-linear ones. Modern particle theories are constructed by choosing the descriptors and choosing groups associated with possible changes of the description of the system.
A fascinating modern research example of scaling arises from the observation that biological systems show scaling laws when they change their size. If you plot the log of the average number of heartbeats a minute for a given species vs. the log of the average mass of that species you get a straight line. That line has been known for almost 100 years, but there has been no explanation of it (on the order of our understanding of how the area changes as we change the length scale) until recently. The answer involves fractals. For an introduction to these ideas, check out the talk by Geoffrey West, one of the discoverers of the explanation.
RETURNS
| University of Maryland | Physics Department | Physics 374 Home |
 |
 |
 |