In the vector space that describes the position of a single particle is moving in three dimensions, our standard vectors (our unit directions) had a useful property -- they were each perpendicular to each other and had a unit length. In a more general linear space, we don't necessarily know what it means to be "perpendicular" or even to say whether it makes sense to say the vector has a "length". In some cases it is useful to do this but in others it is not. [For an example of a vector in which it is not useful to define a length, consider the example of the Gaussian matrix treatment of geometrical optics.]
The tool we use to define both lengths and angles in our 3D space is the dot product. We can see this be the equation that gives the length of a vector:
![]()
and the cosine of the angle between two vectors:
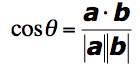
If we can define something analogous to the dot product in a linear space that has analogous properties, we can define lengths and angles. The generalization of the dot product to an arbitrary linear space is called an inner product and a linear space in which an inner product can be defined is called an inner product space .
Just like the dot product, the inner product is a mapping -- an assignment of a scalar to any pair of vectors in the space. We write this as a mapping rule:
I: V x V → S
that is, the inner product is a function rule, I(a,b) that takes two elements of the vector and returns a single scalar. [In our base examples, we write I(a,b) = a⋅b but we are going to something a bit more general soon.]
In order for the inner product to be usable in the way we expect, it has to have certain properties. Check for yourself that the standard dot product satisfies these conditions.
I(a+b,c) = I(a,c) + I(b,c)
I(a,b+c) = I(a,b) + I(a,c)
I(αa,b)=α* I(a,b)
I(a,αb)=α I(a,b)
I(a,b)=I(b,a)*
∀a ∈ V (a ≠ 0) I(a,a) > 0,
I(0,0) = 0 .
(Note that the complex symmetry condition requires that I(a,a) must be real.)
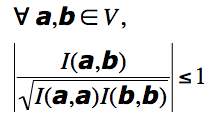
Check for yourself that these conditions hold for the standard dot product in three space.
If we can define such an inner product in whatever space we have -- even if it doesn't "look" geometrical, we can define lengths of vectors and angles between vectors. This lets us define orthonormal bases and do lots of calculations very much more easily that otherwise. This is particularly true in the theory of mechanical waves and in quantum mechanics.
Often, we use Dirac's bra-ket notation for vectors, especially for complex vector spaces since changing from a ket to a bra keeps track of whether we have taken a complex conjugate or not. In such a space, we use a simplified (and satisfying) notation for the inner product: a bra-ket, the angle brackets closing to produce a scalar -- collapsing the two vectors into a number:
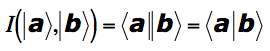
where we commonly replace the double bar that comes from putting the bra and ket together by a single bar.
![]()
| University of Maryland | Physics Department | Physics 374 Home |
|---|---|---|
 |
 |
 |
Last revision 27. October, 2005.