Linear Spaces

Motivation

A lot of what we do in physics deals with linear approximations and linear equations.   Linear approximations are often what we get from the Taylor series, and linear equations have the property of superposition (the sum of two solutions is a solution) so when our physical system has a small oscillation or satisfies superposition, we often describe it using linear equations.   Deciding what degrees of freedom to quantify and how to put them together into an appropriate mathematical structure requires that we both know how the physical system behaves and what are the properties of the mathematical structures associated with linear equations.  

Let's consider two examples of linear spaces:

• the description of one particle moving in three dimensions,
• the description of two particles moving in one dimension.

In the first case, we specify our position by identifying three objects in physical space -- unit vector directions having no length (because the dimensions go with the coordinate), .   A vector then looks like

Our "vector space" consists of all vectors of this form where x, y, and z are real numbers times a dimension of length.

In the second case, we chose two different coordinate systems to describe the motion of the two particles (they had different origins), y₁ and y₂. We wrote an arbitrary vector in this space as

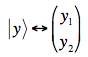
The symbol of the left if what is called "the Dirac ket". (Click here for a detailed discussion of Dirac notation.) We use a "corresponding to" arrow rather than an "=" since the expression on the left is meant to be independent of choice of basis, while the expression on the right explicitly depends on the choice of basis. Note that our first example could be expressed in one on three ways:

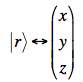
All of these stand for the same thing, but the first (with the ) gives the expression in terms of a specific set of basis vectors. The second, | r >, does not explicitly show the basis and does not depend on it, while the column vector implicitly assumes a(n unspecified) basis.

We are going to be using these examples as analogies or metaphors for other systems that look (physically) nothing like them.   As usual, a careful mathematical definition can tell us when an analogy works and can be used to calculate results and when it can't.

RETURNS

University of Maryland	Physics Department	Physics 374 Home