An example of a vector in which it is not useful to define a length, consider the example of geometrical optics. It is useful (approximations of Gaussian optics) to define a vector in which one component is the distance, h , away from the optical axis (a line running through the center of the optical system) and a second component is the angle, θ , the ray makes with the axis. We can add two of these vectors, or multiply them by scalars, and we have inverses as required by the definition of a linear space.
The value of this representation appears when we consider how we can represent the propagation of the ray or to bending by a lens. In the small angle approximation (where sin θ ≈ θ), these actions can be described in terms of this two component vector ( h, θ) as the action of matrices as seen in the figures below.
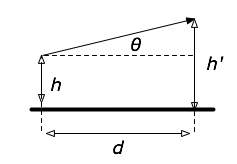
Propagation of a ray by a distance d (in the small angle approximation): the angle stays the same, the height changes.
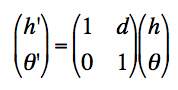
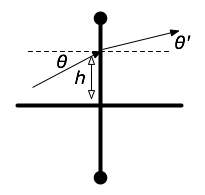
Refraction of a ray at a thin lens of focal length f: the height stays the same, the angle changes.
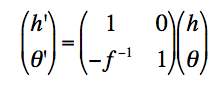
The "length" of this vector is meaningless since you cannot add a length and an angle.
| University of Maryland | Physics Department | Physics 374 Home |
|---|---|---|
 |
 |
 |
Last revision 27. October, 2005.