Complex Numbers

Definitions and Polar Coordinates

The basic definition of complex numbers is that we extend our real number line by adding a number not on that line, the square root of ­1 and all multiples of that by a real number. This leads to two independent (orthogonal) real lines, equivalent to a plane. We write and any complex number as z = x + iy where x and y are real numbers. These are represented on a plane as shown in the figure on the right. The complex number z is represented by the vector shown in the diagram. Polar coordinates are very convenient when working with complex numbers. We define the length of the vector z and the angle it makes with the x axis as:

This gives the inverse relations

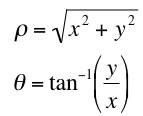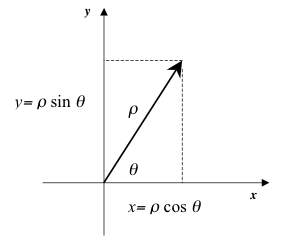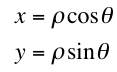
This gives the important representation of a complex number

RETURNS

University of Maryland	Physics Department	Physics 374 Home