Complex Numbers

The Complex Exponential

The representation

appears very frequently so it pays us to look at what it means. In our discussion of the Taylor theorem, we have worked out power series representations of cos and sin so we can put them together and see what we have:

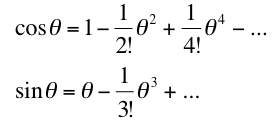
Putting these together as cos θ + i sin θ gives

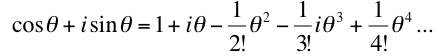
This looks quite systematic. There is a term in every power with a nice systematic set of coefficients ‹ except for the i's. If, however, we notice that i² = -1 we can note that replacing the minus signs by the square of i gives a nice result.

.

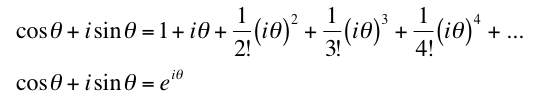The is take care of all the signs and just give us the familiar power series for the exponential. This now gives us an extremely valuable representation for a complex number:

.

The polar representation of the complex number is particularly nice because it's easy to multiply (or divide) that way.

.

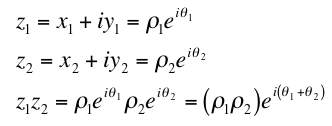You just multiple the lengths and add the angles. What does this algebraic result mean geometrically?

Exercise: To be sure this is consistent, try showing that if you multiply the x-y forms of the complex numbers then the results give the length and angle for the product that the original polar coordinate forms give.

RETURNS

University of Maryland	Physics Department	Physics 374 Home