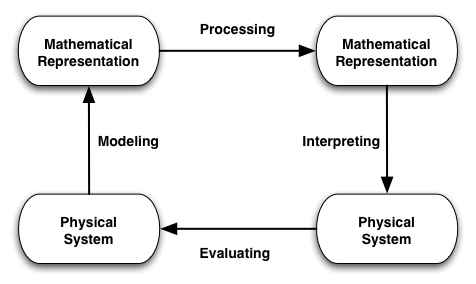
as a guide to the structure of the course. By paying attention to which box we're in or which connection we are talking about, we can be sure that we have not missed thinking about any part of the complex process of applying math to physics.
We'll use this diagram with one or more of the boxes or links highlighted in red to indicate which part of the process a particular exercise or activity pertains to. Here are this single-highlighted icons and their descriptions. We refer to the boxes by the letters "A, B, C, D" and to the links by the numbers "1, 2, 3, 4."
| A. | 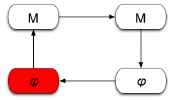 | The Starting Physics: This icon indicates a topic that focuses on selecting what physics to choose to use in describing the system. This might include whether to pay attention to relativity or quantum physics, or some as simple as whether to treat a spring as ideal or an extended body as rigid. Depending on how accurate a result we want, it might be "good enough" to ignore a lot of complicating factors. Learning to "find the physics" in a real world problem is one of the key skills of a good physicist. |
| B. | 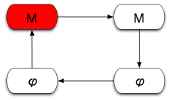 | The Mathematical Structures: Math provides a variety of structures with well-established quantitative relationships that we can use to represent quantities in the physical world. It is important to know a variety of structures that might be used and to well understand their basic assumptions and relations. Often, the "bare" mathematical structures are "enhanced" by our mapping from the physics -- the math has additional properties beyond those specified in the straightforward math. |
| C. | 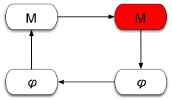 | Mathematical Results: Math structures allow us to process our initial formulation -- perhaps an equation -- into another form -- perhaps a solution -- that we can then interpret in a way we could not when the formulation was in its initial state. Since our "solutions" will often be approximate, we need to understand ways of deciding if our solutions are mathematically correct. This means more than just that our manipulations are correct. It means that our approximations and the errors that result from them are under control (i.e., we know how big they can get and that it is not a problem). |
| D. | 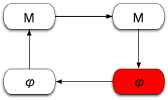 | The Physical Results: Once we have generated our mathematical results, we need to process it back into physics in order to extract the meaning of the math. The physical system we have created with our math may be a caricature of our original system for a number of reasons.
You can probably think of more ways in which we could have gone wrong. In any case, our interpretation in box C can warn us about errors in the system. |
| 1. | 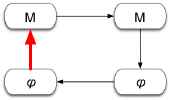 | Modeling: The step involves mapping the physics we have selected to pay attention to into appropriate mathematics. We have to not only assign symbols to physical quantities, we have to decide what kind of "mathematical things" our symbols stand for. (See "Things of Math.") The choice of appropriate mathematical structures is as important as deciding what physics we want to pay attention to. The mathematical structure needs to be appropriate to the physical characteristics. (See "Choosing the Math.") |
| 2. | 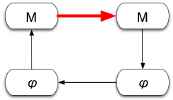 | Processing: In this step we are "doing the math" -- focusing on the solution and/or manipulation of the mathematical equations. We need to have a good sense of how many intermediate steps to put in (to be sure we are doing each step correctly). But we also have to understand the math "down to the roots," that is, know what each mathematical term means so as to be able to take it down to basic definitions when a problem arises. (See "Digging down to the roots.") |
| 3. | 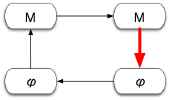 | Interpreting: This link tells us to re-interpret our mathematical results in terms of the physics of the original situation. A math solution is not enough. It has to tell us something about the physical system. Often, interpreting the math in terms of the physics will allow us to understand and make sense of what happened in the formal solution directly from physical principles. You may see how to solve future problems quickly and directly from the physics without having to go through the formal math at all! Eventually, you will begin to blend your mathematical manipulations with a physical picture until the become almost inseparable. |
| 4. | 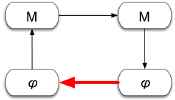 | Evaluation: Our final step is to evaluate whether our process brought us to anb appropriate place. We have to compare the physical results we get from our modeling, mathematical processing, and physical interpretation with what we know about the system we started from. Our result may be obviously wrong. This suggests we have either made a mathematical mistake or left out a crucial piece of physics. Or, our result may lead us to surprising but correct conclusions about our physical system. In any case, the final evaluation of our physical result is an essential (and often ignored) part of using math in physics. |
| University of Maryland | Physics Department | Physics 374 Home |
|---|---|---|
 |
 |
 |
Last revision 2. September, 2005.