Introduction

Motivation

We often describe mathematics as "the language of science." Mathematics is indeed a language, in the sense that it uses arbitrary symbols to convey meaning and has relational rules (a grammar) for operations and transformations. But in science the way we use math is a bit different from what you might see in a math class.

A critical element is how meaning in physics is mapped into and interpreted via mathematical structures. We identify the elements of this process via the following diagram:

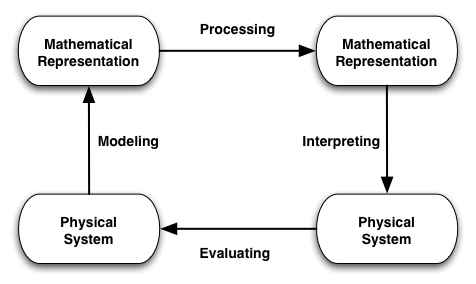
We begin in the lower left with some "things of physics" -- items in the physical world that we want to describe. We then identify the physical elements with "things of math" -- mathematical structures (upper left) that have explicit, well defined relationships and transformation rules. We formulate our physical problem or situation as a problem in math and then process the math to obtain a new statement -- a solution to our problem (upper right). Within the top half of our diagram-- the math half -- we have to understand three things:

The mathematical structures -- their definitions, relations, and basic results
The common transformational processes -- how we "solve" problems in different math structures
Checking our result mathematically -- sometimes we create mathematically approximate solutions and we have to decide if our approximations are good enough.

We then have to bring our math solution "back to the physics" -- that is, we have to interpret our mathematical result physically. Finally, we have to evaluate our physical result, seeing if the model we originally created is "good enough" for whatever purpose we have in mind.

We often think of physics (or any science) as an "exact" description of the real world. But in fact, at every level, we have an approximate model. When we reach some level of accuracy, it's OK to identify our mathematical model with the world as long as we realize that our model is only effectively exact for a limited class of phenomena. We can treat the Newtonian mechanics of rockets and planets in the solar system as "effectively exact" as long as we don't get into situations where we are involving very strong gravitation (black holes), extremely high speeds (a significant fraction of the speed of light), or extremely strong electromagnetic fields (needing Maxwellian dynamics or photons).

RETURNS

University of Maryland	Physics Department	Physics 374 Home

This page prepared by

Edward F. Redish
Department of Physics
University of Maryland
College Park, MD 20742
Phone: (301) 405-6120
Email: redish@umd.edu

Last revision 2. September, 2005.

Introduction

Motivation

Other Related Topics

RETURNS