
Problems for
Intermediate Methods in Theoretical Physics
Edward F. Redish
 |
Problems for |
| Let's first explore the way the density and velocity change as a function of radius. Assume that the spray sets up a steady state of outgoing flow so that the fields describing the fluid density and velocity are independent of time and angle. So they are just a function of radius, ρ(r) and v(r). (a) Rewrite the mass conservation theorem
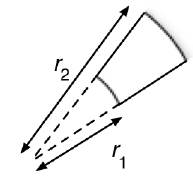
as an integral equation by integrating both sides and applying a vector fundamental theorem of calculus to the side with the gradient operator to get rid of it. (b) Assume that the velocity is constant. If we are ignoring gravity, this is reasonable. What would slow the bits of fluid down? If they are all emitted with the same speed, they should keep the same speed. So we assume v(r) = v0 independent of r. Show what this implies for the density as a function of radius by applying your result from part (a) to the volume consisting of a small angular wedge stretching from a distance r1 to a distance r2 as shown in the figure at the right below.
| 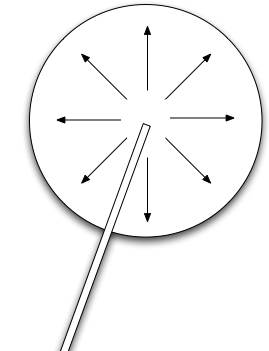 |
|
(c) Write a general theorem analogous to Gauss's law of electrostatics for this fluid. What is your analog of the "charge" in this case? (Hint: Consider the value of the integral over the full sphere for the case in part (b) and consider how it changes with radius. What does this integral mean physically?) (d) If the density of the fluid had to stay constant, what would your integral theorem imply for the velocity as a function of radius?
|  . . |
| University of Maryland | Physics Department | Physics 374 Home |
|---|---|---|
 |
 |
 |
Last revision 5. December, 2004.