
Problems for
Intermediate Methods in Theoretical Physics
Edward F. Redish
 |
Problems for |
(a) Consider trying to shape a string tied down at both ends (y(0,t) = y(L,t) = 0) into a square wave:
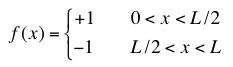
Note we can't really define this function at the joining points since it's not really continuous. We can imagine the rises and falls are sharp, but not infinitely fast.
Expand this function in a Fourier series in the normal modes of the string tied down at both ends by calculating the coefficients fn:
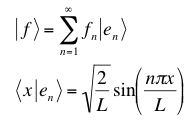
(Hint: Use Dirac notation and the Parity operator to eliminate unneccessary calculations.)
(b) Use a numeric calculation (either Mathematica or a spreadsheet) to calculate and plot the partial sums of the series for the first 6 non-zero terms.
(c) By looking at the shape of f and of the Fourier terms, give a qualitative argument (from symmetry) explaining why the terms that vanish cannot contribute.
(d) The "wiggling ears" that you should find at the edges of the Fourier sums do not go away as you add more and more terms. They settle down in size, but get "squeezed" more and more towards the beginning and end of the 0-L region. This is called the Gibbs phenomenon. What that means is that the partial sums
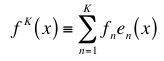
converge in an integrated sense but not in a point-by-point sense; that is:
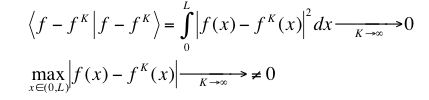 .
.Explain how this can happen in terms of what the functions f K(x) are doing and get an estimate for what the maximum value of |f(x) - f K(x)| for all x is as K → ∞.
| University of Maryland | Physics Department | Physics 374 Home |
|---|---|---|
 |
 |
 |
Last revision 14. November, 2004.