Problems for
Intermediate Methods in Theoretical Physics

Edward F. Redish

Orbital Oscillations

On the first exam we considered the radial motion of a planet in orbit around a star. After eliminating the angular variables, the equation of motion for the radial distance involves an effective radial potential,

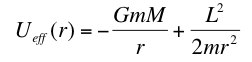
where m is the mass of the planet, M is the mass of the star, G is Newton's universal gravitational constant, and L is the planet's orbital angular momentum. It was then claimed that this equation could be reduced to the dimensionally more convenient form

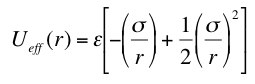
where ε is an energy and σ is a distance. Show that this is the case by finding the explicit form of ε and σ expressed in terms of the original parameters of the problem.

RETURNS

University of MarylandPhysics DepartmentPhysics 374 Home

This page prepared by

Edward F. Redish
Department of Physics
University of Maryland
College Park, MD 20742
Phone: (301) 405-6120
Email: redish@umd.edu

Last revision 14. October, 2004.