
Problems for
Intermediate Methods in Theoretical Physics
Edward F. Redish
 |
Problems for |
| In class we considered the construction of the equations for the motion of two masses hanging on springs as shown in the figure on the right. In this problem, you will solve for the motions. Assume both springs are identical and have the same spring constant, k and the same rest length, L0and that the two masses have the same mass, m. (a) Starting from the physical situation, show that with the proper choice of coordinates, Newton's second law for the two masses can be reduced to: 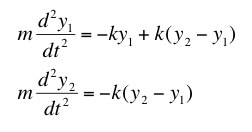 | 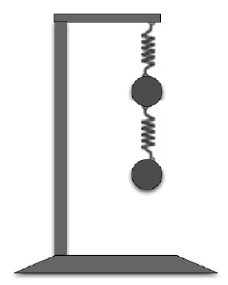 |
(b) Use the complex exponential method to find the natural frequencies and the normal modes of the system.
(c) For each mode discuss the motion physically, explaining why the frequency is what it is.
| University of Maryland | Physics Department | Physics 374 Home |
|---|---|---|
 |
 |
 |
Last revision 12. October, 2004.