
Problems for
Intermediate Methods in Theoretical Physics
Edward F. Redish
 |
Problems for |
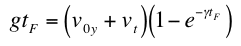
where
vT = mg/b = the terminal velocity
γ = b/m = the damping rate.
where
F(tF) = (v0y + vT)(1 - e-γtF).
Sketch graphs for these two functions as a function of tF.
(b) The solution is at the intersection point of the two graphs. Since f is linear and the Taylor series for F shows that it starts of linearly and then slows its rate of increase, there is a possibility that the graphs will never cross (except at the origin). Let's consider for what values of the parameters there will be a non-zero solution. Assume that the angle is between 0 and 90o and that all of the constants are positive. First discuss from a physical point of view and then demonstrate your result mathematically.
(c) Expand F to second order in γtF ( = tF/tb, therefore a dimensionless number) and solve for tF.
(d) Show that if b = 0 you get the known result for time of flight, tF = 2v0y/g.
(e) Notice that if you put back the original constants (b, m, g) your solution is not second order in b. Arrange your constants so that b is grouped with other constants to make a dimensionless number and find the correction to tF to first order in this dimensionless number.
| University of Maryland | Physics Department | Physics 374 Home |
|---|---|---|
 |
 |
 |
Last revision 12. October, 2004.