Random vs Systematic Error
Random
errors in experimental measurements are caused by unknown and
unpredictable changes in the experiment. These changes may occur in the
measuring instruments or in the environmental conditions.
Examples of causes of random errors are:
- electronic noise in the circuit of an electrical instrument,
- irregular changes in the heat loss rate from a solar collector due to changes in the wind.
Random errors often have a Gaussian normal distribution (see
Fig. 2). In such cases statistical methods may be used to analyze the
data. The mean m of a number of measurements of the same quantity is the best estimate of that quantity, and the standard deviation s of the measurements shows the accuracy of the estimate. The standard error of the estimate m is s/sqrt(n), where n is the number of measurements.
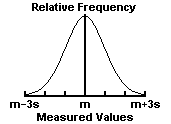
Fig. 2. The Gaussian normal distribution. m = mean of measurements. s =
standard deviation of measurements. 68% of the measurements lie in the
interval m - s < x < m + s; 95% lie within m - 2s < x < m + 2s; and 99.7% lie within m - 3s < x < m + 3s.
The precision of a measurement is how close a number of
measurements of the same quantity agree with each other. The precision
is limited by the random errors. It may usually be determined by
repeating the measurements.
Systematic errors in experimental observations usually come from the measuring instruments. They may occur because:
- there is something wrong with the instrument or its data handling system, or
- because the instrument is wrongly used by the experimenter.
Two types of systematic error can occur with instruments having a linear response:
- Offset or zero setting error in which the instrument does not read zero when the quantity to be measured is zero.
- Multiplier or scale factor error in which the instrument consistently reads changes in the quantity to be measured greater or less than the actual changes.
These errors are shown in Fig. 1. Systematic errors also occur with
non-linear instruments when the calibration of the instrument is not
known correctly.
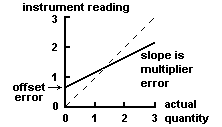
Fig. 1. Systematic errors in a linear instrument (full line).
Broken line shows response of an ideal instrument without error.
Examples of systematic errors caused by the wrong use of instruments are:
- errors in measurements of temperature due to poor thermal contact
between the thermometer and the substance whose temperature is to be
found,
- errors in measurements of solar radiation because trees or buildings shade the radiometer.
The accuracy of a measurement is how close the
measurement is to the true value of the quantity being measured. The
accuracy of measurements is often reduced by systematic errors, which
are difficult to detect even for experienced research workers.
Taken from R. H. B. Exell,
www.jgsee.kmutt.ac.th/exell/PracMath/ErrorAn.htm


