- (a)
-
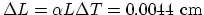 .
.
- (b)
- Since
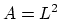 ,
,
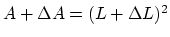 where
where
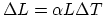 , you can express
, you can express
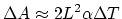 . So
. So
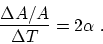
- (c)
- Some air bubbles get trapped inside the liquid after you shake the bottle. If you suddenly open the bottle, the air expands due to sudden drop of the pressure (at a much higher rate than the liquid), which pushes some of the liquid out of the bottle.
- 2)
- (a)
- Equate the heat loss of the metal and the heat gain of the
liquid:
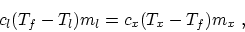
then the specific heat of the metal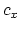 is
is
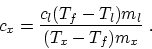
- (b)
- You only need the info on melting of silver. With specific heat
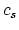 and the specific heat of fusion
and the specific heat of fusion 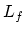 , the total heat
needed to melt the silve of mass
, the total heat
needed to melt the silve of mass 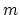 at temperature
at temperature 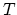 is
is
![\begin{displaymath}Q= m[c_s(T_m-T)+L_f]~,\end{displaymath}](img54.gif)
where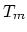 is the melting point. Then
is the melting point. Then
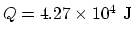 .
.
- (c)
- In constant volume processes, no work is done by the gas, and therefore,
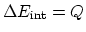 . Then
. Then
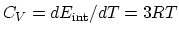 per mol.
per mol.- 3)
- (a)
- In one cycle,
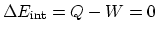 , which means that
the total net heat added is equal to the total net work done by the
gas. Since the cycle is counterclockwise, the net work is negative
(negative heat),
, which means that
the total net heat added is equal to the total net work done by the
gas. Since the cycle is counterclockwise, the net work is negative
(negative heat),
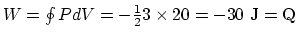 .
.
- (b) to (d):
- The internal energy difference in this case is
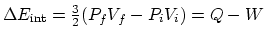 , and
, and 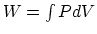 , from which you can find the heat
, from which you can find the heat  .
(b) An isobaric process:
.
(b) An isobaric process:
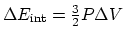 and
and
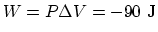 . So
. So
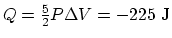 .
(c) An isovolumetric process:
.
(c) An isovolumetric process:
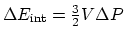 , and
, and 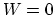 . Then
. Then
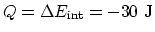 .
(d)
.
(d)
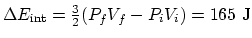 ,
and
,
and
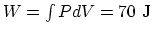 . Then
. Then
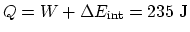 .
.
- 4)
- (a)
- The mass of one mole of the air is
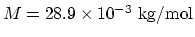 . The specific heat is then
. The specific heat is then
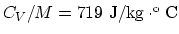 .
.
- (b)
- From the equipartition theorem,
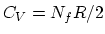 where
where 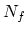 is
the number of degrees of freedom of each molecule. So
is
the number of degrees of freedom of each molecule. So 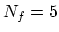 in
this case. For the kinetic energy only, however, the average value is
still the same as that of an ideal monatomic gas,
in
this case. For the kinetic energy only, however, the average value is
still the same as that of an ideal monatomic gas,
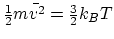 . Therefore,
. Therefore,
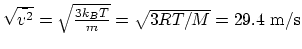 .
.
- (c)
- Since the weight of the piston would not change over this
process, this is an isobaric process, with the well-known relation
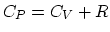 . The air inside the cylinder is
. The air inside the cylinder is
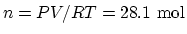 , The total heat needed to be added is
, The total heat needed to be added is
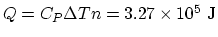 .
.
- 5)
- (a)
- Since
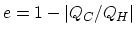 , you only need to calculate the total
added heat and the total extracted heat. It is helpful to draw a
diagram and number each stroke. The processes 1 and 2 adds heat to the
engine, 3 and 4 extracts heat. (
, you only need to calculate the total
added heat and the total extracted heat. It is helpful to draw a
diagram and number each stroke. The processes 1 and 2 adds heat to the
engine, 3 and 4 extracts heat. (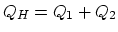 ,
, 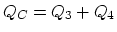 .)
.)
Since 1 is an isovolumetric process and 2 is an isothermal process,
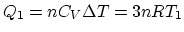 , and
, and
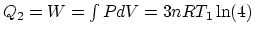 .
So
.
So
![$Q_H = 3nRT_1 [1+\ln (4) ]$](img88.gif) .
.
Similarly, 3 is an isovolumetric process and 4 is an isothermal process. So
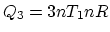 ,
,
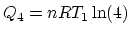 , and finally
, and finally
![$Q_C= nRT_1[3+\ln(4)]$](img91.gif) .
.
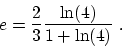
- (b)
- The total entropy change of a reversible cycle is zero. In realistic engines with irreversible processes, the entropy change of the total system is always positive.



Next: About this document ... Up: Mid-term (PHYS262, Summer 2001) Previous: Questions Hyok-Jon Kwon
2001-08-10