| Physics 121 |
Final Exam (Solution) | December 15, 2005 |
Instructions: Answer all five questions on these sheets.
Problem I (50 points) is standard multiple-choice, graded only by chosen answer (work needs not be shown).
For Problems II - V (12+12+16+10 points) show your work, including any equations you used, or explain in words how you arrived at numerical answers.
The exam lasts 2 hours 50 minutes.
I. Multiple Choice. Use "Scantron" sheet 0. Please sign the Pledge on your "Scantron" sheet. It applies to the entire exam.
- Which of the following is not a vector quantity?
a. temperature
b. velocity
c. acceleration
d. displacement
- In one-dimensional motion, the average speed of an object that moves from one place to another and then back to its original place has which of the following properties?
a. It is positive.
b. It is negative.
c. It is zero.
d. It can be positive, negative, or zero.
- A cheetah can run at approximately 30 m/s and a gazelle at 25 m/s. If both animals are running at full speed, with the gazelle 50.0 m ahead, how long before the cheetah catches its prey?
a. 10 s
b. 25 s
c. 30 s
d. 50 s
- Jeff throws a ball straight up. For which situation is the vertical velocity zero?
a. on the way up
b. at the top
c. on the way back down
d. none of the above
- In the case of constant acceleration, the average velocity equals the instantaneous velocity:
a. at the beginning of the time interval.
b. at the end of the time interval.
c. half-way through the time interval.
d. three-fourths of the way through the time interval.
- A rock is thrown straight up with an initial velocity of 19.6 m/s. What time interval elapses between the rock's being thrown and its return to the original launch point? (Acceleration due to gravity is 9.80 m/s².)
a. 4.00 s
b. 5.00 s
c. 8.00 s
d. 10.0 s
- Human reaction time is usually about 0.20 s. If your lab partner holds a ruler between your finger and thumb and releases it without warning, how far can you expect the ruler to fall before you catch it? The nearest value is:
a. 4.0 cm. c. 16 cm.
b. 9.8 cm. d. 20 cm.
- Vector A is 3 m long and vector B is 4 m long. The length of the sum of the vectors must be:
a. 5 m.
b. 7 m.
c. 12 m.
d. some value from 1 m to 7 m.
- A plane is moving due north, directly towards its destination. Its airspeed is 200 mph. A constant breeze is blowing from west to east at 40 mph. How long will it take for the plane to travel 200 miles north?
a. one hour
b. more than one hour
c. less than one hour
d. more information is needed
- A 7.0-kg bowling ball experiences a net force of 7.0 N. What will be its acceleration?
a. 36 m/s²
b. 7.0 m/s²
c. 5.0 m/s²
d. 1.0 m/s²
- As I slide a box at constant speed up a frictionless slope, pulling parallel to the slope, the tension in the rope will be:
a. greater than the tension would be if the box were stationary.
b. greater than the weight of the box.
c. equal to the weight of the box.
d. less than the weight of the box.
- I use a rope 2.00 m long to swing a 10.0-kg weight around my head with constant angular velocity, in an exact circle. The tension in the rope is 20.0 N. In half a revolution how much work is done by the rope on the weight?
a. 40.0 J
b. 126 J
c. 251 J
d. 0
- When an object is dropped from a tower, what is the effect of the air resistance as it falls?
a. does positive work
b. increases the object's kinetic energy
c. increases the object's potential energy
d. None of the above choices are valid.
- Two blocks are released from the top of a building. One falls straight down while the other slides down a smooth ramp. If all friction is ignored, which one is moving faster when it reaches the bottom?
a. The block that went straight down.
b. The block that went down the ramp.
c. They both will have the same speed.
d. Insufficient information to work the problem.
- A Hooke's law spring is compressed a distance d and is used to launch a mass m vertically to a height h above its starting position. Under double the compression, the spring is now used to launch the mass. How high does the mass now rise above its starting position?
a. 2 h
b. 1.41 h
c. 3 h
d. 4 h
- A force of 5.0 N is applied to a 20-kg mass on a horizontal frictionless surface. As the speed of the mass increases at a constant acceleration, the power delivered to it by the force:
a. remains the same.
b. increases.
c. decreases.
d. doubles every 4.0 seconds.
- A ball with original momentum +4.0 kg m/s hits a wall and bounces straight back without losing any kinetic energy. The change in momentum of the ball is:
a. 0.
b. -4.0 kg m/s.
c. 8.0 kg m/s.
d. -8.0 kg m/s.
- A moderate force will break an egg. However, an egg dropped on the road usually breaks, while one dropped on the grass usually doesn't break. This is because for the egg dropped on the grass:
a. the change in momentum is greater.
b. the change in momentum is less.
c. the time interval for stopping is greater.
d. the time interval for stopping is less.
- A billiard ball collides in an elastic head on collision with a second identical ball. What is the kinetic energy of the system after the collision compared to that before collision?
a. the same as
b. one fourth
c. twice
d. four times
- Popeye, of mass 70 kg, has just downed a can of spinach. He accelerates quickly and stops Bluto, of mass 700 kg (Bluto is very dense), who is charging in at 10 m/s. What was Popeye's speed?
a. 10 m/s
b. 31 m/s
c. 50 m/s
d. 100 m/s
- Starting from rest, a wheel undergoes constant angular acceleration for a period of time T. At which of the following times does the average angular acceleration equal the instantaneous angular acceleration?
a. 0.50 T
b. 0.67 T
c. 0.71 T
d. all of the above
- A point on the rim of a 0.25-m-radius fan blade has centripetal acceleration of 0.20 m/s². Find the centripetal acceleration of a point 0.05 m from the center of the same wheel.
a. 0.01 m/s²
b. 0.02 m/s²
c. 0.04 m/s²
d. 0.08 m/s²
- When a point on the rim of a 0.30-m-radius wheel experiences a centripetal acceleration of 4.0 m/s², what tangential acceleration does that point experience?
a. 1.2 m/s²
b. 2.0 m/s²
c. 4.0 m/s²
d. Cannot determine with the information given.
- Consider a point on a bicycle tire that is momentarily in contact with the ground as the bicycle rolls across the ground with constant speed. The direction for the acceleration for this point at that moment is:
a. upward.
b. down toward the ground.
c. forward.
d. at that moment the acceleration is zero
- Two children seat themselves on a seesaw. The one on the left has a weight of 400 N while the one on the right weighs 300 N. The fulcrum is at the midpoint of the seesaw. If the child on the left is not at the end but is 1.50 m from the fulcrum and the seesaw is balanced, what is the torque provided by the weight of the child on the right? (positive torque is counterclockwise)
a. 600 N·m c. -600 N·m
b. 450 N·m d. -450 N·m
- If a net torque is applied to an object, that object will experience:
a. a constant angular speed.
b. an angular acceleration.
c. a constant moment of inertia.
d. an increasing moment of inertia.
- The Earth moves about the Sun in an elliptical orbit. As the Earth moves closer to the Sun, which of the following best describes the Earth Sun system's moment of inertia?
a. decreases
b. increases
c. remains constant
d. none of the above choices are valid
- A uniform solid sphere rolls down an incline of height 3 m after starting from rest. In order to calculate its speed at the bottom of the incline, one needs to know:
a. the mass of the sphere.
b. the radius of the sphere.
c. the mass and the radius of the sphere.
d. no more than is given in the problem.
- A solid disk of radius R rolls down an incline in time T. The center of the disk is removed up to a radius of R/2. The remaining portion of the disk with its center gone is again rolled down the same incline. The time it takes is:
a. T.
b. more than T.
c. less than T.
d. requires more information than given in the problem to figure out.
- The Earth's gravity exerts no torque on a satellite orbiting the Earth in an elliptical orbit. Compare the motion of the satellite at the point nearest the Earth (perigee) to the motion at the point farthest from the Earth (apogee). At these two points:
a. the tangential velocities are the same.
b. the angular velocities are the same.
c. the angular momenta are the same.
d. the kinetic energies are the same.
- A 15 000-N car on a hydraulic lift rests on a cylinder with a piston of radius 0.20 m. If a connecting cylinder with a piston of 0.040-m radius is driven by compressed air, what force must be applied to this smaller piston in order to lift the car?
a. 600 N
b. 1 500 N
c. 3 000 N
d. 15 000 N
- As ice floats in water, about 10% of the ice floats above the surface of the water. If we float some ice in a glass of water, what will happen to the water level as the ice melts?
a. The water level will rise 10% of the volume of the ice that melts.
b. The water level will rise, but not as much as the 10% indicated in answer A.
c. The water level will remain unchanged.
d. The water level will become lower.
- A large stone is resting on the bottom of the swimming pool. The normal force of the bottom of the pool on the stone is equal to the:
a. weight of the stone.
b. weight of the water displaced.
c. sum of the weight of the stone and the weight of the displaced water.
d. difference between the weight of the stone and the weight of the displaced water.
- What is the temperature of a system in thermal equilibrium with another system made up of ice and water at one atmosphere of pressure?
a. 0°F
b. 273 K
c. 0 K
d. 100°C
- What happens to a given mass of water as it is cooled from 4°C to zero?
a. expands
b. contracts
c. vaporizes
d. neither expands, contracts, nor vaporizes.
- A steel plate has a hole drilled through it. The plate is put into a furnace and heated. What happens to the size of the inside diameter of a hole as its temperature increases?
a. increases
b. decreases
c. remains constant
d. becomes elliptical
- What happens to a volume of water when its temperature is reduced from 8°C to 4°C?
a. density increases
b. density decreases
c. density remains constant
d. vaporizes
- What happens to its moment of inertia when a steel disk is heated?
a. It increases.
b. It decreases.
c. It stays the same.
d. It increases for half the temperature increase and then decreases for the rest of the temperature increase.
- An ideal gas is confined to a container with constant volume and the amount of gas is constant. By what factor will the pressure change if the absolute temperature triples?
a. 1/9
b. 1/3
c. 3.0
d. 9.0
- The absolute temperature of an ideal gas is directly proportional to which of the following properties, when taken as an average, of the molecules of that gas?
a. speed
b. momentum
c. mass
d. kinetic energy
- Which of the following statements is true?
a. A hot object contains a lot of heat.
b. A cold object contains only a little heat.
c. Objects do not contain heat.
d. Statements a and b are true.
- A slice of bread contains about 100 kcal. If specific heat of a person were 1.00 kcal/kg·°C, by how many °C would the temperature of a 70.0kg person increase if all the energy in the bread were converted to heat?
a. 2.25°C
b. 1.86°C
c. 1.43°C
d. 1.00°C
- Iced tea is made by adding ice to 1.0 kg of hot tea, initially at 90°C. How many kg of ice, initially at 0°C, are required to bring the mixture to 10°C? (Lf = 80 cal/g, cw = 1 cal/g×°C)
a. 1.8 kg
b. 1.4 kg
c. 1.0 kg
d. 0.6 kg
- In cloud formation, water vapor turns into water droplets which get bigger and bigger until it rains. This will cause the temperature of the air in the clouds to:
a. get warmer.
b. get cooler.
c. will not affect the temperature of the air in the clouds.
d. There is no air in clouds.
- A system is acted on by its surroundings in such a way that it receives 50 J of heat while simultaneously doing 20 J of work. What is its net change in internal energy?
a. 70 J
b. 30 J
c. zero
d. -30 J
- In an isothermal process for an ideal gas system (where the internal energy doesn’t change), which of the following choices best corresponds to the value of the work done on the system?
a. its heat intake
b. twice its heat intake
c. the negative of its heat intake
d. twice the negative of its heat intake
- The maximum theoretical thermodynamic efficiency of a heat engine operating between hot and cold reservoirs is a function of which of the following?
a. hot reservoir temperature only
b. cold reservoir temperature only
c. both hot and cold reservoir temperatures
d. None of the above choices are valid.
- According to the second law of thermodynamics, which of the following applies to the heat received from a high temperature reservoir by a heat engine operating in a complete cycle?
a. must be completely converted to work
b. equals the entropy increase
c. converted completely into internal energy
d. cannot be completely converted to work
- In which system is heat usually transferred from the cooler part to the warmer part?
a. a stove as it heats up water
b. a refrigerator that is running
c. an electric fan that is running
d. none of the above, because it is impossible to transfer heat in this manner
- A 2.00-kg block of ice is at 0°C and 1 atm while it melts completely to water. What is its change in entropy? (For ice, Lf = 3.34 × 105 J/kg)
a. zero
b. 584 J/K
c. 1 220 J/K
d. 2 450 J/K
Short answer questions. Show your work!
II. Kinematics
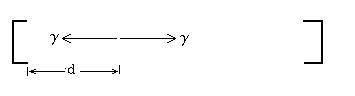 Some elementary particles can be detected only by what they leave behind when they decay. Such a particle (called π0) decays into two particles (called γ's) which move at the speed of light, 3×108 m/s, traveling in opposite directions. To find where the π0 was -- that is, the place where the γ's started -- we place two γ-counters so that each receives one of the γ's, as in the figure. The distance between the counters is 2 m, and the left counter responded 10-9 seconds before the right counter. What is the distance d?
Some elementary particles can be detected only by what they leave behind when they decay. Such a particle (called π0) decays into two particles (called γ's) which move at the speed of light, 3×108 m/s, traveling in opposite directions. To find where the π0 was -- that is, the place where the γ's started -- we place two γ-counters so that each receives one of the γ's, as in the figure. The distance between the counters is 2 m, and the left counter responded 10-9 seconds before the right counter. What is the distance d?
The distance to one counter is d, that to the other counter is 2 - d (all distances in meters), so the flight time to one is d/c, and to the other (2-d)/c, where c is the speed of light.
The difference between these is the given 10−9s, so
10−9 = (2-d)/c - d/c. Multiply by c: 10−9 × 3×108 = 0.3 = (2 - d) - d = 2 - 2d, and hence d = ½(2 - 0.3) = 0.85 m
- At t = 0 a bus is moving towards its stop on a straight road with a speed 15 m/s. The bus stop is 320 m ahead of the bus, and the bus arrives there at t = 20 s (so its speed is zero at t = 20 s). In that 20 s time interval, did the bus
- not accelerate nor decelerate
- only accelerate
- only decelerate
- both accelerate and decelerate?
Explain your choice, giving a cogent reason why it must be right.
The bus must certainly decelerate to come to a stop. Suppose it did not accelerate, then in 20 s it could go at most (15 m/s)(20s) = 300m. But since the stop is further away than that, it must have accelerated before decelerating.
Another way to argue is by computing the vav = 320m/20s = 16 m/s. The bus cannot go at an average speed of 16 m/s by only decelerating from 15 m/s.
- The speedometer on a car's dashboard reads on a linear scale. The scale 4.5 in long, with speed 0 at 0 cm, and speed 150 km/h = 42 m/s at 4.2 in. The car is accelerating at 2 m/s². What is the speed in inches/second of the accelerometer "needle" (that is, the pointer indicating the present speed) with respect to the car's dashboard?
Since it does not matter at what speed the car is going, suppose it starts at speed 0, and accelerates for 1 s. It is then going at 2 m/s. The speedometer needle started at speed 0, hence position 0, and reached position 0.2 in after the 1 sec. (Since 42 m/s is indicated on the scale at 4.2 in, 2 m/s is indicated at 0.2 in). Hence the needle's speed is 0.2 in/1 s = 0.2 in/s.
III. Dynamics
- You are twirling your keys of mass 1 kg on their key string in a vertical circle of radius 10 cm = 0.1 m. At the top of their circular trajectory the string tension just reaches zero (the keys are in free fall at that moment).
- What is the keys' speed at the bottom of the circle?
- What is their acceleration at the bottom?
- What is the tension in the string when the keys are at the bottom?
i. In free fall, gravity provides the centripetal force, so mg = mvtop²/R. (This yields vtop = 1 m/s if g = 10 m/s², but it is better not to solve for v at this time because we want next to use conservation of energy)
Conservation of energy says (with v = speed at bottom)
½mv² = ½mvtop² + mg(2R) = ½(mgR) + mg(2R) = (5/2)mgR, so v = √(5gR) = 2.21 m/s
ii. There is no horizontal acceleration (angular velocity reaches maximum magnitude at bottom, so momentarily does not change). The etire acceleration is vertical, therefore centripetal, and determined by the speed alone, a = v²/R = 5gR/R = 5g = 49 m/s²
iii. The centripetal force consists of string tension (up) and gravity (down) so
mv²/R = T − mg T = 5mgR/R + mg = 6 mg = 58.8 N
- A car (treated as a point particle) is moving with constant speed along an S-shaped track as shown. On the figure, at the points indicated, accurately draw the car's acceleration vector. Use an arbitrary scale, but keep it the same at all the points.
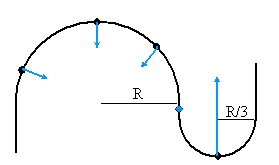
- A roll of newsprint (paper for newspaper) has radius R, and paper is fed from it into the printing press with a constant speed v.
- What is the roll's angular velocity (magnitude as formula, direction description in words)?
- How much time does it take for one revolution? (formula in terms of R and v)
- If the paper's thickness is t, the radius decreases by t in one revolution. What is the angular velocity after this decrease by t? (formula in terms of R, v, t)
- What is therefore the angular acceleration of the roll? (slightly complicated formula in terms of R, v, t)
i. ω = v/R direction along axis of rotation. If paper is coming off the bottom of the roll and the paper moves to the right, ω points out at the viewer.ii. One revolution moves a length 2πR of paper; to move that distance with velocity v takes a time Δt = 2πR/v.
iii. Since the radius is now R-t, the angular velocity is ω' = v/(R-t)
| iv. α = Δω/Δt = (ω'−ω)/Δt = [v/R-t − v/R] (v/2πR) = | v²t
2πR²(R-t) |
IV. Fluids
- A cart containing a crocodile can roll on a level frictionless track.
- Initially the cart and crocodile are at rest, with the croc at the left wall of the cart. The croc now starts to crawl to the right inside the cart. Will the cart move? If so, in what direction? What law of physics tells you?
The cart will move, in order to conserve momentum. Frictionless track implies no external force, so the croc's momentum to the right has to be balanced by the cart's momentum to the left.
- Next the cart is filled with water and starts out again at rest, with the croc swimming near the cart's left wall. Then the croc swims to the right. Will the cart move in this case? Why?
In this case the cart does not move. While swimming the crocodile displaces and equal weight, and hence equal mass, of water. The water and croc are in the enclosed volume of the cart, so when the croc swims to the right, and equal mass of water moves to the left, and momentum of croc + water is conserved, without the cart having to move.
However, this assumes that there is no friction between water and cart. If there is, there is no reason why the cart should not share in the momentum.
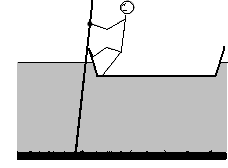 Mr and Mrs Johnson (the ones who recently moved) are in a boat, and their motor died. They have no oars, but there is a long rod that will reach to the bottom of the lake. Mr Johnson suggests to stick the rod vertically from the back of the boat into the mud on the lake's bottom, and pull forward on the top of the rod. Mrs Johnson (as usual thinking about forces) predicts that this won't work, because Mr. Johnson will be pushing backward with his feet as hard as he is pulling forward with his hands. Mr. Johnson (as usual thinking about work) argues "I'll be doing work, that must convert into K.E., hence we and the boat will move".
Mr and Mrs Johnson (the ones who recently moved) are in a boat, and their motor died. They have no oars, but there is a long rod that will reach to the bottom of the lake. Mr Johnson suggests to stick the rod vertically from the back of the boat into the mud on the lake's bottom, and pull forward on the top of the rod. Mrs Johnson (as usual thinking about forces) predicts that this won't work, because Mr. Johnson will be pushing backward with his feet as hard as he is pulling forward with his hands. Mr. Johnson (as usual thinking about work) argues "I'll be doing work, that must convert into K.E., hence we and the boat will move".
- Will the boat move? Explain
The boat will move. If it did not, we could use the point of contact between pole and boat as a fixed origin for calculating torques, which would have to add to zero. To balance Mr. Johnson's torque, there must be a foce at the bottom end of the pole. But this force would be an external force on the boat+pole system, a contradiction to the assumption that the boat (+pole) does not move.
To show this without resorting to proof by contradiction, we must take torques about the bottom of the pole, which is certain to be fixed. Because the lever arms of the boat and of Mr Johnson's hand are unequal, and their torques must be the same (we can assume negligible mass, and hence negligible moment of inertia, of the pole), the two forces must be unequal; their difference will propel the boat.
- If yes, think of the boat, occupants, and pole as one system and neglect friction with the water. Where does the force to the system get applied?
If no, where does the work go that Mr. Johnson does?The force is applied at the point where the pole is stuck in the mud of the lake bottom.
If you answered that the boat does not move, a consistent answer would be that any work Mr. Johnson does goes into bending the pole.
- A block, of density greater than that of water, is resting on a plane. The coefficient of friction between plane and block is μ = 1. The plane is tilted until the critical angle is reached at which the block begins to slip.
- What is this critical angle (between plane and horizontal)?
Since tan θ = μ = 1, θ = 45°.
- The experiment is repeated under water. The coefficient of friction remains the same. What is now the critical angle? Explain.
It is the same, 45°. The buoyant force is vertical, opposite to the gravitational force. For statics, it is as if the mass of the block were reduced. But the equation for θ is independent of the block's mass.
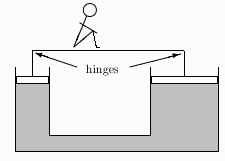 Two cylindrical vessels containing a fluid, one twice the radius of the other, are connected at the bottom, and each carry a piston at the top. The pistons are connected by hinges to a horizontal bar. Where on the bar can a person sit (that is, where can a vertical force be applied to the bar) so the bar does not tilt? (specify what fraction of the bar's length from left resp. right end)
Two cylindrical vessels containing a fluid, one twice the radius of the other, are connected at the bottom, and each carry a piston at the top. The pistons are connected by hinges to a horizontal bar. Where on the bar can a person sit (that is, where can a vertical force be applied to the bar) so the bar does not tilt? (specify what fraction of the bar's length from left resp. right end)At equilibrium the pressure on the two pistons is the same, so the force is proportional to the piston's area, 4 times as large on the right than on the left. So the person should be 4 times further from the left piston than from the right (unlike what is shown in the figure). The person should be 1/5 of the bar's length from the right end.
V. Lab
Note: The phrase "human error" should not appear in the answer to this question.
John performs an experiment in which he measures the period of a pendulum. He wishes to find the relationship between the period of the pendulum and its length.
Being a good experimentalist, John measures the time taken for five complete swings, and then obtains the period by dividing this number by five.
- Why does John time five rather than just one swing?
To reduce the random error in the measurement, and to increase precision. (The method may still result in an inaccurate answer if systematic error is involved.)
After performing the experiment for several lengths, with many trials per length, John creates the following graph:
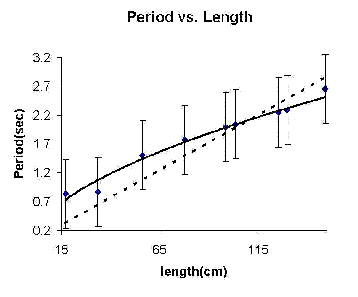 |
The error bars are a measure
of the distribution of the
data collected for each length |
John knows that the relationship should be T ~ √L (——), but realizes that his graph also admits
a linear fit (· · · · ·).
- What does this say about the accuracy of the experiment?
The average values recorded are very close to the true values, as can be seen by looking at the T ~ √L line. Therefore, the experiment is accurate.
- What does this say about the precision of the experiment?
The large error bars indicate that the experiment is not precise.
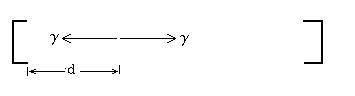 Some elementary particles can be detected only by what they leave behind when they decay. Such a particle (called π0) decays into two particles (called γ's) which move at the speed of light, 3×108 m/s, traveling in opposite directions. To find where the π0 was -- that is, the place where the γ's started -- we place two γ-counters so that each receives one of the γ's, as in the figure. The distance between the counters is 2 m, and the left counter responded 10-9 seconds before the right counter. What is the distance d?
Some elementary particles can be detected only by what they leave behind when they decay. Such a particle (called π0) decays into two particles (called γ's) which move at the speed of light, 3×108 m/s, traveling in opposite directions. To find where the π0 was -- that is, the place where the γ's started -- we place two γ-counters so that each receives one of the γ's, as in the figure. The distance between the counters is 2 m, and the left counter responded 10-9 seconds before the right counter. What is the distance d?
 Mr and Mrs Johnson (the ones who recently moved) are in a boat, and their motor died. They have no oars, but there is a long rod that will reach to the bottom of the lake. Mr Johnson suggests to stick the rod vertically from the back of the boat into the mud on the lake's bottom, and pull forward on the top of the rod. Mrs Johnson (as usual thinking about forces) predicts that this won't work, because Mr. Johnson will be pushing backward with his feet as hard as he is pulling forward with his hands. Mr. Johnson (as usual thinking about work) argues "I'll be doing work, that must convert into K.E., hence we and the boat will move".
Mr and Mrs Johnson (the ones who recently moved) are in a boat, and their motor died. They have no oars, but there is a long rod that will reach to the bottom of the lake. Mr Johnson suggests to stick the rod vertically from the back of the boat into the mud on the lake's bottom, and pull forward on the top of the rod. Mrs Johnson (as usual thinking about forces) predicts that this won't work, because Mr. Johnson will be pushing backward with his feet as hard as he is pulling forward with his hands. Mr. Johnson (as usual thinking about work) argues "I'll be doing work, that must convert into K.E., hence we and the boat will move". Two cylindrical vessels containing a fluid, one twice the radius of the other, are connected at the bottom, and each carry a piston at the top. The pistons are connected by hinges to a horizontal bar. Where on the bar can a person sit (that is, where can a vertical force be applied to the bar) so the bar does not tilt? (specify what fraction of the bar's length from left resp. right end)
Two cylindrical vessels containing a fluid, one twice the radius of the other, are connected at the bottom, and each carry a piston at the top. The pistons are connected by hinges to a horizontal bar. Where on the bar can a person sit (that is, where can a vertical force be applied to the bar) so the bar does not tilt? (specify what fraction of the bar's length from left resp. right end)